What is Quantum Entanglement?

Interconnected Quantum World

Quantum entanglement is a phenomenon where the quantum states of two or more particles are interconnected and cannot be described independently of each other, even when the particles are separated by a large distance. The measurement outcomes performed on such states are strongly correlated, stronger than what is possible within classical systems. In the context of quantum computing, entanglement allows quantum computers to manipulate many qubits in a single operation, instead of manipulating each qubit individually. However, the extent to which entanglement contributes to the computational speedup of quantum computers is not yet fully understood.

Quantum entanglement is a phenomenon where the quantum states of two or more particles are interconnected and cannot be described independently of each other

Product States vs Entangled States

To obtain a better understanding of entanglement, it is important to examine the notion of states and combined systems in quantum mechanics.

Product States

Product states describe systems composed of multiple subsystems where the state of each individual subsystem can be described independently. Mathematically, the state of the combined system can then be expressed as a tensor product of states of the individual subsystems. For the simple case of two qubits, A and B, where each one is in the state ∣ψ⟩A and ∣ψ⟩B respectively, the state of the combined system of the two is expressed as the tensor product of the two individual qubit states: ​

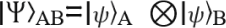
∣Ψ⟩AB=∣ψ⟩A ⊗∣ψ⟩B


Here, ⊗ represents the tensor product, which combines states in a manner that permits the independent evolution of each state. In product states, measuring one part of the system does not influence the outcome of measuring the other part.

Let’s look at an example of a product state, when two qubits are each prepared in an equal superposition of the basis states ∣0⟩_and ∣1⟩. In such a case, the state of the joint system of A and B is the tensor product of two qubit states A and B.



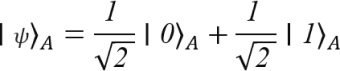
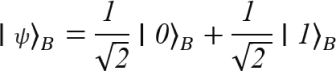
When we take the tensor product of ∣ψ⟩_A and ∣ϕ⟩B, we get the product state


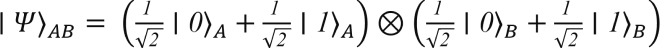
which results in


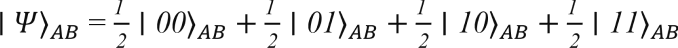
Which represents an equally weighted superposition of basis states of the combined system ∣00⟩_AB, ∣01⟩_AB, ∣10⟩_AB, and ∣11⟩_AB. This state ∣Ψ⟩_AB is separable because it can be written in the form of a tensor product of basis states.

In general, any state that can be expressed as a tensor product expression of basis states is called separable.


Entangled States

In entangled states, on the other hand, the joint quantum states of two or more particles cannot be described independently of each other, even when the particles are separated by large distances. Mathematically, if a joint system composed of subsystems A and B is in an entangled state, it cannot be factored into a tensor product of two independent single-particle states. This is, in fact, the definition of an entangled state: A state ∣Ψ⟩_AB is called entangled if it is not separable (in any basis).


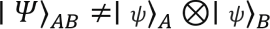
Instead, entangled states are represented by a sum of product states.

We will analyse the features of entangled states with an example. A commonly used entangled state for two qubits, is the so called Bell state ∣Φ^+⟩:


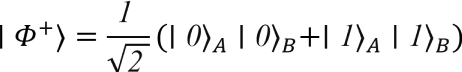
In this state, the outcomes of a measurement on qubit A are correlated with the measurement outcomes of qubit B. When we obtain ∣0⟩_A as the outcome of a measurement on qubit A, we know that qubit B is in state ∣0⟩_B, and analogously for ∣1⟩.

This type of correlation with respect to a single basis, here the ∣0⟩/∣1⟩ basis, is not yet so special. A separable state such as ∣0⟩_A∣0⟩_B, or ∣1⟩_A∣1⟩_B, or a mixed state with terms ∣0⟩_A∣0⟩_B and ∣1⟩_A∣1⟩_B would also exhibit similar correlations when measured in the standard ∣0⟩/∣1⟩ basis. However, if we measure these states in the diagonal ∣+⟩/∣-⟩ basis instead, the measurement outcomes would be statistically random and uncorrelated. In contrast, if we measure the entangled Bell state ∣Φ^+⟩ in the diagonal basis, we still obtain perfectly correlated results, even though each individual measurement result is intrinsically random! You can verify this yourself by expanding these states in the diagonal basis.


EPR Paradox


This correlation of measurement outcomes on entangled states, is what lies at the core of the so-called EPR paradox, introduced by Einstein, Podolsky, and Rosen in 1935 [2]. The EPR paradox was a thought experiment designed to question whether quantum mechanics provides a complete description of physical reality. In a nutshell, they argued that the inherent randomness and notion of entangled states in quantum mechanics indicated that the quantum theory was incomplete, suggesting the existence of “hidden variables” that – while inaccessible to the experimenter – determine the outcome of each measurement. This perspective is known as local realism.

Local realism is based on two fundamental principles:

Locality: The idea that an object is only directly influenced by its immediate surroundings and not by distant surroundings.

Realism: The belief that physical quantities have well defined values even when they are not being measured or observed.

A little bit like the moon, that is also there when we don’t look at it.


In the EPR paper, they considered two particles in an entangled state. Their derived correlations appeared to violate the principle of locality and the interpretation of the measured physical quantity as an element of physical reality, creating the paradox. This famously led Einstein to describe entanglement as “spooky action at a distance.”

Bell’s Theorem and Bell Test


In 1964, physicist John Bell proposed a theorem stating that any theory based on local hidden variables yields different predictions for the outcomes of certain experiments compared to quantum mechanics. These experiments, now famously known as Bell tests, involve measuring the properties of entangled particles in different directions [3].

If the correlations between the measurement outcomes in experiments with entangled states exceed a specific limit (known as Bell’s inequality), the predictions of quantum mechanics are confirmed, and local realism can be ruled out (Let that sink in). In other words, if Bell’s inequality is violated, then “spooky action at a distance” is fact, indicating that the universe is fundamentally non-local.

Since Bell’s theorem was proposed, numerous modern versions of Bell test experiments have been carried out. In all well-controlled tests, the results have consistently violated Bell’s inequality, providing strong empirical evidence against local realism and supporting quantum mechanics.

Nobel Prizes


In 2022, the Nobel Prize in Physics recognized the significant contributions of John Clauser, Alain Aspect, and Anton Zeilinger to the field of quantum physics. The prize was awarded “for experiments with entangled photons, establishing the violation of Bell inequalities, and pioneering quantum information science.” John Clauser further developed John Bell’s ideas and conducted an experiment that supported quantum mechanics by violating a Bell inequality.

Alain Aspect improved upon Clauser’s experiment, closing an important loophole in the experiment. Anton Zeilinger and his research group demonstrated experimental quantum teleportation for the first time, a phenomenon that allows the transfer of a quantum state from one particle to another at a distance using entanglement as a resource.

These groundbreaking works have significantly advanced our understanding of quantum entanglement and its potential applications [4].

References:

[1] https://learning.quantum.ibm.com/course/basics-of-quantum-information/multiple-systems
[2] https://cds.cern.ch/record/405662/files/PhysRev.47.777.pdf
[3] https://cds.cern.ch/record/111654/files/vol1p195-200_001.pdf
[4] https://www.nobelprize.org/prizes/physics/2022/press-release/