Was ist Quantenverschränkung?

Vernetzte Quantenwelt

Quantenverschränkung ist ein Phänomen, bei dem die Quantenzustände von zwei oder mehr Teilchen miteinander verbunden sind und nicht unabhängig voneinander beschrieben werden können, selbst wenn die Teilchen durch eine große Entfernung getrennt sind. Die Messergebnisse solcher Zustände sind stark korreliert, stärker als dies in klassischen Systemen möglich ist. Im Zusammenhang mit Quantencomputern ermöglicht die Verschränkung es Quantencomputern, viele Qubits in einer einzigen Operation zu manipulieren, anstatt jedes Qubit einzeln zu manipulieren. Das Ausmaß, in dem die Verschränkung zur Beschleunigung der Rechenleistung von Quantencomputern beiträgt, ist jedoch noch nicht vollständig bekannt.

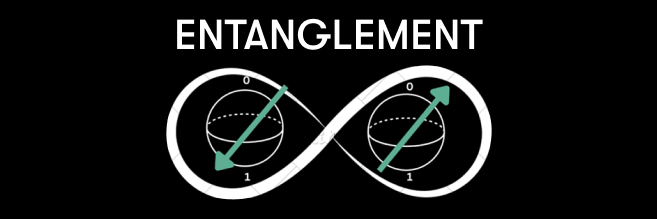
Produktzustände vs. verschränkte Zustände

Um die Verschränkung besser zu verstehen, ist es wichtig, den Begriff der Zustände und kombinierten Systeme in der Quantenmechanik zu untersuchen.

Produkt Staaten

Produktzustände beschreiben Systeme, die aus mehreren Teilsystemen bestehen, wobei der Zustand jedes einzelnen Teilsystems unabhängig beschrieben werden kann. Mathematisch gesehen kann der Zustand des kombinierten Systems dann als Tensorprodukt der Zustände der einzelnen Teilsysteme ausgedrückt werden. Für den einfachen Fall von zwei Qubits, A und B, von denen sich jedes im Zustand _∣ψ⟩A bzw. _∣ψ⟩B befindet, wird der Zustand des kombinierten Systems der beiden als das Tensorprodukt der beiden individuellen Qubit-Zustände ausgedrückt:

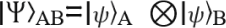
Dabei steht ⊗ für das Tensorprodukt, das die Zustände so kombiniert, dass die unabhängige Entwicklung jedes Zustands möglich ist. Bei Produktzuständen hat die Messung eines Teils des Systems keinen Einfluss auf das Ergebnis der Messung des anderen Teils.

Schauen wir uns ein Beispiel für einen Produktzustand an, wenn zwei Qubits jeweils in einer gleichwertigen Überlagerung der Basiszustände ∣0⟩_und∣1⟩präpariert werden. In einem solchen Fall ist der Zustand des gemeinsamen Systems von A und B das Tensorprodukt der beiden Qubit-Zustände A und B.

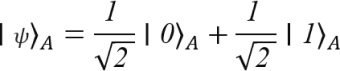
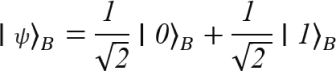
Wenn wir das Tensorprodukt von _{∣ψ⟩_A} und∣ϕ⟩nehmen _B erhalten wir den Produktzustand

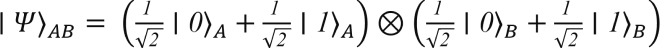
was dazu führt, dass

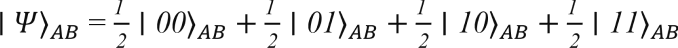
die eine gleich gewichtete Überlagerung der Basiszustände des kombinierten Systems ∣00⟩_AB, ∣01⟩_AB, ∣10⟩_AB und ∣11⟩_AB darstellt. Dieser Zustand ∣Ψ⟩_AB ist trennbar, weil er in Form eines Tensorprodukts von Basiszuständen geschrieben werden kann.

Im Allgemeinen wird jeder Zustand, der sich als Tensorprodukt von Basiszuständen ausdrücken lässt, als trennbar bezeichnet.

Verstrickt Staaten

Bei verschränkten Zuständen hingegen können die gemeinsamen Quantenzustände von zwei oder mehr Teilchen nicht unabhängig voneinander beschrieben werden, selbst wenn die Teilchen durch große Entfernungen getrennt sind. Wenn sich ein gemeinsames System aus den Teilsystemen A und B in einem verschränkten Zustand befindet, kann es mathematisch gesehen nicht in ein Tensorprodukt aus zwei unabhängigen Einzelteilchenzuständen zerlegt werden. Dies ist in der Tat die Definition eines verschränkten Zustands: Ein Zustand ∣Ψ⟩_AB wird verschränkt genannt, wenn er nicht trennbar ist (in jeder Basis).

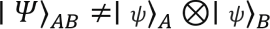
Stattdessen werden die verschränkten Zustände durch eine Summe von Produktzuständen dargestellt.

Wir werden die Eigenschaften von verschränkten Zuständen anhand eines Beispiels analysieren. Ein häufig verwendeter verschränkter Zustand für zwei Qubits ist der so genannte Bell-Zustand ∣Φ^+⟩:

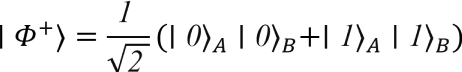
In diesem Zustand sind die Ergebnisse einer Messung an Qubit A mit den Messergebnissen von Qubit B korreliert. Wenn wir ∣0⟩_A als Ergebnis einer Messung an Qubit A erhalten, wissen wir, dass sich Qubit B im Zustand ∣0⟩_B befindet, und analog für ∣1⟩.

Diese Art der Korrelation in Bezug auf eine einzige Basis, hier die ∣0⟩/∣1⟩-Basis, ist noch nicht so speziell. Ein trennbarer Zustand wie ∣0⟩_A∣0⟩_B oder ∣1⟩_A∣1⟩_B oder ein gemischter Zustand mit den Termen ∣0⟩_A∣0⟩_B und ∣1⟩_A∣1⟩_B würde ebenfalls ähnliche Korrelationen aufweisen, wenn er auf der Standardbasis ∣0⟩/∣1⟩ gemessen wird. Wenn wir diese Zustände jedoch stattdessen auf der diagonalen ∣+⟩/∣-⟩-Basis messen, wären die Messergebnisse statistisch zufällig und unkorreliert. Wenn wir dagegen den verschränkten Bell-Zustand ∣Φ^+⟩ in der diagonalen Basis messen, erhalten wir immer noch perfekt korrelierte Ergebnisse, auch wenn jedes einzelne Messergebnis an sich zufällig ist! Sie können dies selbst überprüfen, indem Sie diese Zustände in der diagonalen Basis erweitern.

EPR-Paradoxon

Diese Korrelation von Messergebnissen bei verschränkten Zuständen ist der Kern des sogenannten EPR-Paradoxons, das 1935 von Einstein, Podolsky und Rosen eingeführt wurde [2]. Das EPR-Paradoxon war ein Gedankenexperiment, das die Frage aufwerfen sollte, ob die Quantenmechanik eine vollständige Beschreibung der physikalischen Realität liefert. Kurz gesagt, argumentierten sie, dass die inhärente Zufälligkeit und der Begriff der verschränkten Zustände in der Quantenmechanik darauf hindeuten, dass die Quantentheorie unvollständig ist, was auf die Existenz “versteckter Variablen” hindeutet, die – obwohl sie für den Experimentator nicht zugänglich sind – das Ergebnis jeder Messung bestimmen. Diese Perspektive wird als lokaler Realismus bezeichnet.

Der lokale Realismus basiert auf zwei Grundprinzipien:

Lokalität: Die Vorstellung, dass ein Objekt nur von seiner unmittelbaren Umgebung direkt beeinflusst wird und nicht von einer entfernten Umgebung.

Realismus: Der Glaube, dass physikalische Größen genau definierte Werte haben, auch wenn sie nicht gemessen oder beobachtet werden.

Ein bisschen wie der Mond, der auch da ist, wenn wir ihn nicht ansehen.

In der EPR-Arbeit betrachteten sie zwei Teilchen in einem verschränkten Zustand. Ihre abgeleiteten Korrelationen schienen das Lokalitätsprinzip und die Interpretation der gemessenen physikalischen Größe als Element der physikalischen Realität zu verletzen, wodurch das Paradoxon entstand. Dies veranlasste Einstein, die Verschränkung als “spukhafte Fernwirkung” zu bezeichnen.

Bell’s Theorem und Bell-Test

1964 schlug der Physiker John Bell ein Theorem vor, das besagt, dass jede Theorie, die auf lokalen verborgenen Variablen basiert, andere Vorhersagen für die Ergebnisse bestimmter Experimente liefert als die Quantenmechanik. Bei diesen Experimenten, die heute als Bell-Tests bekannt sind, werden die Eigenschaften von verschränkten Teilchen in verschiedenen Richtungen gemessen [3].

Wenn die Korrelationen zwischen den Messergebnissen in Experimenten mit verschränkten Zuständen einen bestimmten Grenzwert überschreiten (bekannt als Bellsche Ungleichung), werden die Vorhersagen der Quantenmechanik bestätigt und lokaler Realismus kann ausgeschlossen werden (lassen Sie das auf sich wirken). Mit anderen Worten: Wenn die Bellsche Ungleichung verletzt wird, dann ist die “spukhafte Fernwirkung” eine Tatsache, was darauf hindeutet, dass das Universum im Grunde nicht lokal ist.

Seitdem das Bellsche Theorem vorgeschlagen wurde, wurden zahlreiche moderne Versionen der Bell-Test-Experimente durchgeführt. In allen gut kontrollierten Tests haben die Ergebnisse durchweg die Bellsche Ungleichung verletzt, was einen starken empirischen Beweis gegen den lokalen Realismus liefert und die Quantenmechanik unterstützt.

Nobelpreise

Im Jahr 2022 würdigte der Nobelpreis für Physik die bedeutenden Beiträge von John Clauser, Alain Aspect und Anton Zeilinger auf dem Gebiet der Quantenphysik. Der Preis wurde “für Experimente mit verschränkten Photonen, den Nachweis der Verletzung der Bell-Ungleichungen und die Pionierarbeit in der Quanteninformatik” verliehen. John Clauser entwickelte die Ideen von John Bell weiter und führte ein Experiment durch, das die Quantenmechanik unterstützte, indem es eine Bellsche Ungleichung verletzte.

Alain Aspect verbesserte Clausers Experiment und schloss damit eine wichtige Lücke in dem Experiment. Anton Zeilinger und seine Forschungsgruppe haben zum ersten Mal die experimentelle Quantenteleportation demonstriert, ein Phänomen, das die Übertragung eines Quantenzustands von einem Teilchen auf ein anderes über eine Entfernung hinweg ermöglicht, indem es die Verschränkung als Ressource nutzt.

Diese bahnbrechenden Arbeiten haben unser Verständnis der Quantenverschränkung und ihrer potenziellen Anwendungen erheblich erweitert [4].

Referenzen:

[1] https://learning.quantum.ibm.com/course/basics-of-quantum-information/multiple-systems
[2] https://cds.cern.ch/record/405662/files/PhysRev.47.777.pdf
[3] https://c ds.cern.ch/record/111654/files/vol1p195-200_001.pdf
[4] https://www.nobelprize.org/prizes/physics/2022/press-release/